Implemented RTL code in Verilog for bit ripple carry adder, carry lookahead adder, and carry select adder with equal group size and different group size; Compared all adders in their timing, area, and power performances. Ran logic simulation, wrote Perl script to run synthesis, ran gate-level simulation, and performed STA using Primetime.
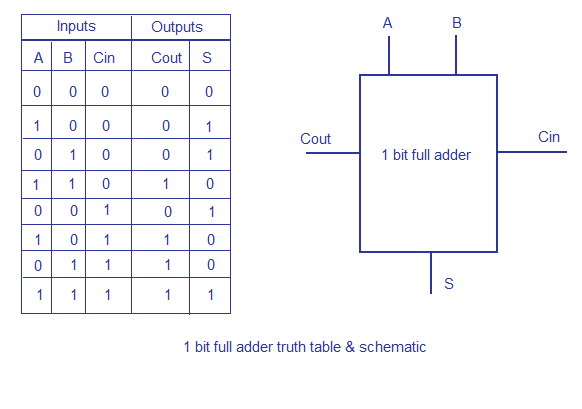
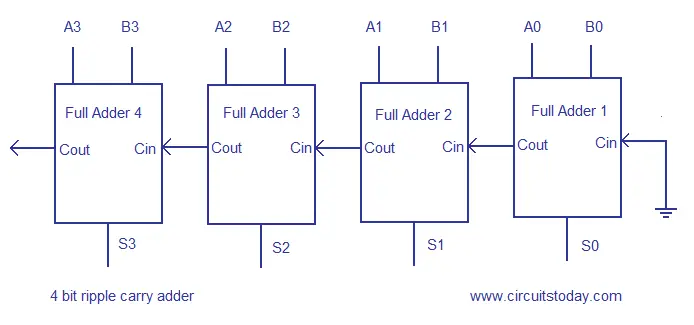
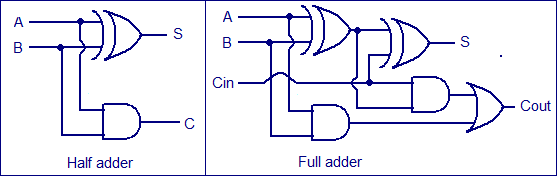
The simplest way to build an N-bit carry propagate adder is to chain together N full adders. The Cout of one stage acts as the Cin of the next stage. We can build a full adder first, and then chain four full adders together to build a 4-bit adder, and chain 4-bit adders together to build a bit adder, and then to build a bit adder.
The 4-bit is consisted of four 1-bit adders. Cout from previous adder is propagated to next adder as Cin. Four full-adder modules are instantiated, as M1, M2, M3, and M4 respectively. The Verilog for 4-bit adder is in the following:. Four 4-bit adder modules are instantiated, as M1, M2, M3, and M4 respectively. The Verilog for bit adder is in the following:.
The design has clock and reset signal as inputs. So, we need to include this feature in the top level bit ripple carry adder. The inputs and outputs are listed in the following:. Clock and reset are for sequential block; op1 and op2 are two bit inputs. Sum is a bit output and crout stands for carry out, which is 1 bit. The following part instantiates four bit ripple carry adders, stores the sum result into sumbuffer, and stores carry out result into croutbuffer.
This is the sequential part. This is 2 bit ripple carry adder circuit using lt reset. When reset goes to 1, output sum and crout are reset to 0, and input buffers a and b are reset to 0. Otherwise, at every positive edge of clock signal, a and b take values from op1 and op2, sum and crout take values from sumbuffer and croutbuffer. Large ripple-carry adders are slow is that the carry signals must propagate through every bit in the adder.
A carry- lookahead adder CLA is another 2 bit ripple carry adder circuit using lt of carry propagate adder that solves this problem by dividing the adder into blocks and providing circuitry to quickly determine the carry out of a block 2 bit ripple carry adder circuit using lt soon as the carry in is known. CLAs use generate G and propagate P signals that describe how a column or block determines the carry out.
The ith column of an adder is guaranteed to generate a carry 2 bit ripple carry adder circuit using lt if Ai and Bi are both 1. The column is said to propagate a carry if it produces a carry out whenever there is a carry in.
In equation form, Ci can be computed this way:. A block propages a carry if all the columns in the block propagage the carry. For a 4-bit carry lookahead adder, the propagate logic is. In this way, we can quickly compute the carry out of the block, Ci, using the carry in to the block Cj. Ripple Carry Adder The simplest way to build an N-bit carry propagate adder is to chain together N full adders.
Binance isn't based in UK, the taxman has no power to demand to see everyone's trades on an offshore business. Marketcap bitcoin. Iu0027ve put: use 15 balance but it doesnu0027t work, it didnu0027t even buy thecoins.