Buy liquitex
42 comments
Bitcoin and cryptocurrency technologies a comprehensive introduction review
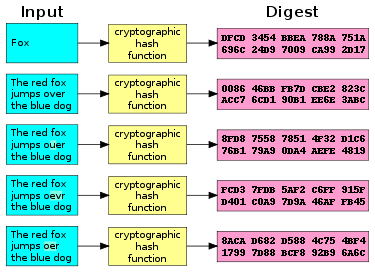
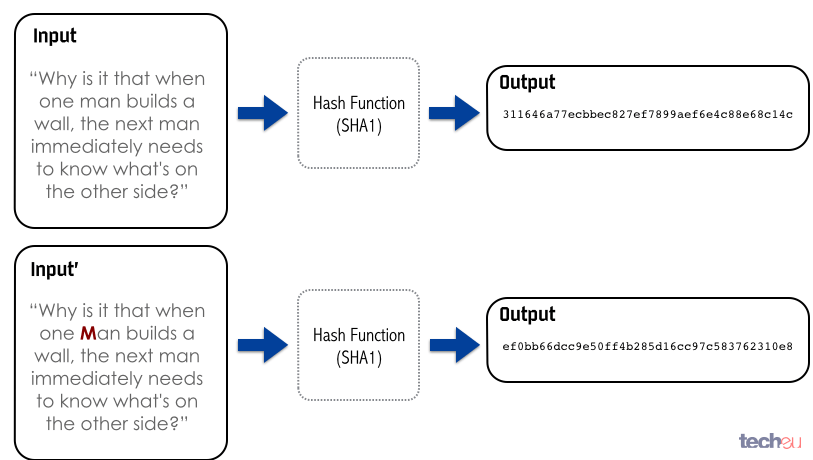
The task is to find a nonce which, as part of the bitcoin block header , hashes below a certain value. This is a brute force approach to something-like-a preimage attack on SHA The process of mining consists of finding an input to a cryptographic hash function which hashes below or equal to a fixed target value.
It is brute force because at every iteration the content to be hashed is slightly changed in the hope to find a valid hash; there's no smart choice in the nonce.
The choice is essentially random as this is the best you can do on such hash functions. In this article I propose an alternative mining algorithm which does not perform a brute force search but instead attacks this problem using a number of tools used in the program verification domain to find bugs or prove properties of programs, see as example [9]. Namely, a model checker backed by a SAT solver are used to find the correct nonce or prove the absence of a valid nonce. In contrast to brute force, which actually executes and computes many hashes, my approach is only symbolically executing the hash function with added constraints which are inherent in the bitcoin mining process.
This is not the first time SAT solvers are used to analyse a cryptographic hash. Mate Soos et al have done interesting research on extending SAT solvers for cryptographic problems [1]; Iilya Mironov and Lintao Zhang generated hash collisions using off-the-shelf SAT solvers [2]; and many others, e. However, to the best of my knowledge, this is the first description of an application of SAT solving to bitcoin mining.
I do not claim that it is a faster approach than brute force, however it is at least theoretically more appealing. To aid understanding, I will introduce some basic ideas behind SAT solving and model checking. Please see the references for a better introduction to SAT solving [11] and bounded model checking [12]. Boolean Satisfiability SAT is the problem of finding an assignment to a boolean formula such that the whole formula evaluates to true.
As easy as it may sound, it is one of the hard, outstanding problems in computer science to efficiently answer this decision problem. There is a large and thriving community around building algorithms which solve this problem for hard formulas. Actually, each year there is a competition held where the latest, improved algorithms compete against each other on common problems. Thanks to a large number of competitors, a standard input format DIMACS , and the easy way of benchmarking the performance of SAT solvers there have been massive improvements over the last 10 years.
Today, SAT solvers are applied to many problem domains which were unthinkable a few years ago for example they are used in commercial tools [5, 7] to verify hardware designs.
Wikipedia summarises the algorithm well:. A literal is simply a variable or its negation. A clause is a disjunction of literals. CNF is then any formula which purely consists of conjunctions of clauses.
DPLL then consists of a depth-first search of all possible variable assignments by picking an unassigned variable, inferring values of further variables which logically must follow from the current assignment, and resolving potential conflicts in the variable assignments by backtracking.
A common application of SAT solving is bounded model checking [12], which involves checking whether a system preserves or violates a given property, such as mutual exclusive access to a specific state in the system.
Model checkers such as CBMC [5] directly translate programming languages like C into CNF formulas, in such a way that the semantics of each language construct such as pointers arithmetic, memory model, etc are preserved. Clearly, this is quite involved and is done in a number of steps: As visible in the figure, the property which should be checked for violations is expressed as an assertion.
If it is not possible to make the formula true then the property is guaranteed to hold. Most importantly, in case of satisfiability, the model checker can reconstruct the variable assignment and execution trace called counterexample which leads to the violation using the truth variable assignments provided by the solver.
Using the above tools we can attack the bitcoin mining problem very differently to brute force. We take an existing C implementation of sha from a mining program and strip away everything but the actual hash function and the basic mining procedure of sha sha block.
The aim of this is that with the right assumptions and assertions added to the implementation, we direct the SAT solver to find a nonce. Instead of a loop which executes the hash many times and a procedure which checks if we computed a correct hash, we add constraints that when satisfied implicitly have the correct nonce in its solution.
The assumptions and assertions can be broken down to the following ideas: The nonce is modelled as a non-deterministic value The known structure of a valid hash, i. Instead of a loop that continuously increases the nonce, we declare the nonce as a non-deterministic value.
This is a way of abstracting the model. In model checking, non-determinism is used to model external user input or library functions e. The nonce can be seen as the only "free variable" in the model.
Bitcoin mining programs always have to have a function which checks whether the computed hash is below the target see here for an example. We could do the same and just translate this function straight to CNF, however there is a much better and more declarative solution than that in our case. Instead, we can just assume values which we know are fixed in the output of the hash.
This will restrict the search space to discard any execution paths where the assumptions would not be true anymore. Because we are not in a brute force setting, but a constraint solving setting this is very simple to express. We assume the following: Only compute hashes which have N bytes [N depends on the target] of leading zeros.
It might seem unintuitive to "fix" output variables to certain values, however remember that the code is not executed in a regular fashion but translated as a big formula of constraints.
Assumptions on the outputs will result in restrictions of the input -- in our case this means only valid nonces will be considered. This serves three purposes: Again, in comparison, brute force just blindly computes hashes with no way of specifying what we are looking for. The SAT-based solution only computes hashes that comply with the mining specification of a valid hash.
The most important part is defining the assertion, or the property P as it is called in the section above. The key idea here is that the counterexample produced by the model checker will contain a valid nonce given a clever enough assertion.
A bounded model checker is primarily a bug finding tool. You specify the invariant of your system, which should always hold, and the model checker will try to find an execution where this invariant is violated i.
That is why the P above is negated in the formula. Thus, the invariant, our P, is set to "No valid nonce exists". This is naturally expressed as the assertion. Which the model checker will encode to its negation as "a valid nonce does exist", i. If a satisfiable solution is found, we will get an execution path to a valid nonce value.
In reality, this is encoded more elegantly. Since the leading zeros of a hash are already assumed to be true, all that remains to be asserted is that the value of the first non-zero byte in the valid hash will be below the target at that position. Again, we know the position of the non-zero byte for certain because of the target. For example, if our current target is the following:. Then the following assertion states that a certain byte in state[6] of the hash has to be above 0x As the assertion is negated, the SAT solver will be instructed to find a way to make the flag equal to 0.
The only way this can be done is by playing with the only free variable in the model -- the nonce. In that way, we just translated the bitcoin mining problem into SAT solving land. Combining the ideas from the above sections results in a conceptual SAT-based bitcoin mining framework.
In pseudo C code this looks as follows:. The advantage of using the built-in solver is that, in case of satisfiability, the model checker can easily retrieve a counterexample from the solution which consists of all variable assignments in the solution. A violation of the assertion implies a hash below the target is found. Let us inspect a counterexample when run on the genesis block as input.
At state below, the flag was found to be 0 which violates the assertion. Moving upwards in the execution trace we find a valid hash in state Finally, the value of the non-deterministically chosen nonce is recovered in state The implementation of the above program generates a large CNF formula with about ' variables and ' clauses. In order to evaluate its performance I generated two benchmark files where one has a satisfiable solution and the other does not. I restricted the nonce range the possible values to be chosen to values for each file.
The files are available on the following github project. Unsurprisingly, the solvers are not capable of solving this problem efficiently as of now.
However, it is interesting to see the differences in runtime. This is interesting as Cryptominisat has been specifically tuned towards cryptographic problems as it is able to detect and treat xor clauses differently to normal clauses [1]. This feature is extensively used in this case, in the above run the solver found over non-binary xor clauses. The crypto-focused optimisations of Cryptominisat could potentially have helped in solving this more efficiently than the other solvers.
However, it is very surprising that ZChaff wins the SAT challenge with a good margin to the next solver. ZChaff is the oldest of all solvers presented here, the version I am using is 9 years old. This could indicate that the heuristics applied by modern SAT solvers do not help in this particular instance.
Generally, it is not known what makes a SAT instance hard or easy, which leaves only speculation or analysis of the stats provided by the SAT solvers to come to useful conclusions. I could speculate that the avalanche effect of the hash function produces a very structured CNF formula with high dependencies between clauses and variables.
Perhaps a higher degree of randomisation applied by heuristics performs less well than straight-forward DPLL. I leave this to someone with more SAT solving knowledge to decide.
While the performance numbers are not great compared to GPU mining we have to keep in mind that this is entirely unoptimised and there are many ways of how this can be sped up. To give an idea of the performance gains that can be achieved with little effort I am going to use a combination of features:. In this experiment, I am going to use Cryptominisat as it performed well in the UNSAT challenge and has a large number of parameters with parameter tuning and slicing.
The restrict parameter is a way to only branch on the 32 most active variables which is intended for cryptography key search -- 32 was picked arbitrarily. In the second row, I tried running it with the plain parameter which deactivates all simplification heuristics, in order to see if the speculations around the ZChaff-speed improvement could also apply to Cryptominisat.